Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 80, pp. 1-11.
Laplace transform and generalized Hyers-Ulam
stability of linear differential equations
Qusuay H. Alqifiary, Soon-Mo Jung
Abstract:
By applying the Laplace transform method, we
prove that the linear differential equation
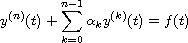
has the generalized Hyers-Ulam stability, where
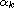 is
a scalar, y and f are n times continuously differentiable
and of exponential order.
is
a scalar, y and f are n times continuously differentiable
and of exponential order.
Submitted March 5, 2014. Published March 21, 2014.
Math Subject Classifications: 44A10, 39B82, 34A40, 26D10.
Key Words: Laplace transform method; differential equations;
generalized Hyers-Ulam stability.
Show me the PDF file (234 KB),
TEX file, and other files for this article.
 |
Qusuay H. Alqifiary
Department of Mathematics,
University of Belgrade, Belgrade, Serbia.
University of Al-Qadisiyah, Al-Diwaniya, Iraq
email: qhaq2010@gmail.com
|
|---|
 |
Soon-Mo Jung
Mathematics Section
College of Science and Technology
Hongik University, 339--701 Sejong, Korea
email: smjung@hongik.ac.kr
|
|---|
Return to the EJDE web page


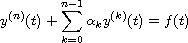
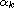 is
a scalar, y and f are n times continuously differentiable
and of exponential order.
is
a scalar, y and f are n times continuously differentiable
and of exponential order.