If
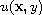 is an infinity harmonic
function, i.e., a viscosity solution to the equation
is an infinity harmonic
function, i.e., a viscosity solution to the equation
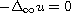 in
in
 then the function
then the function
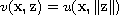 is infinity harmonic
in the set
is infinity harmonic
in the set
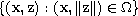 (provided
(provided
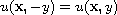 ).
).
Gustaf Gripenberg
Abstract:
If
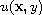 is an infinity harmonic
function, i.e., a viscosity solution to the equation
is an infinity harmonic
function, i.e., a viscosity solution to the equation
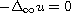 in
in
 then the function
then the function
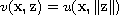 is infinity harmonic
in the set
is infinity harmonic
in the set
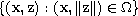 (provided
(provided
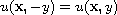 ).
).
Submitted May 21, 2015. Published June 10, 2015.
Math Subject Classifications: 35J60, 35J70.
Key Words: Infinity harmonic; extension; viscosity solution.
Show me the PDF file (196 KB), TEX file for this article.
 |
Gustaf Gripenberg Department of Mathematics and Systems Analysis Aalto University P.O. Box 11100, FI-00076 Aalto, Finland email: gustaf.gripenberg@aalto.fi |
|---|
Return to the EJDE web page