Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 285, pp. 1-23.
Exponential P-stability of stochastic nabla-dynamic equations on
disconnected sets
Huu Du Nguyen, Thanh Dieu Nguyen, Anh Tuan Le
Abstract:
The aim of this article is to consider the existence of solutions,
finiteness of moments, and exponential p-stability of stochastic
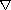 -dynamic
equations on an arbitrary closed subset of
-dynamic
equations on an arbitrary closed subset of
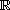 ,
via Lyapunov functions. This work can be considered as a unification
and generalization of works dealing with random difference and
stochastic differential equations.
,
via Lyapunov functions. This work can be considered as a unification
and generalization of works dealing with random difference and
stochastic differential equations.
Submitted April 4, 2013. Published November 11, 2015.
Math Subject Classifications: 60H10, 34A40, 34D20, 39A13, 34N05.
Key Words: Differential operator; dynamic equation; exponential stability;
Ito's formula; Lyapunov function.
Show me the PDF file (324 KB),
TEX file for this article.
 |
Huu Du Nguyen
Faculty of Mathematics, Mechanics, and Informatics
University of Science-VNU
334 Nguyen Trai, Thanh Xuan, Hanoi, Vietnam
email: dunh@vnu.edu.vn
|
|---|
 |
Thanh Dieu Nguyen
Department of Mathematics, Vinh University
182 Le Duan, Vinh, Nghe An, Vietnam
email: dieunguyen2008@gmail.com
|
|---|
 |
Anh Tuan Le
Faculty of Fundamental Science
Hanoi University of Industry
Tu Liem district, Ha Noi, Vietnam
email: tuansl83@yahoo.com
|
|---|
Return to the EJDE web page
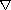 -dynamic
equations on an arbitrary closed subset of
-dynamic
equations on an arbitrary closed subset of
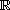 ,
via Lyapunov functions. This work can be considered as a unification
and generalization of works dealing with random difference and
stochastic differential equations.
,
via Lyapunov functions. This work can be considered as a unification
and generalization of works dealing with random difference and
stochastic differential equations.


