Electron. J. Differential Equations,
Vol. 2016 (2016), No. 289, pp. 1-16.
Multiple solutions for biharmonic elliptic problems
with the second Hessian
Fei Fang, Chao Ji, Binlin Zhang
Abstract:
In this article, we study the biharmonic elliptic problem with
the secondnd Hessian
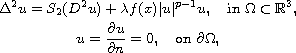
where
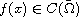 is a sign-changing weight function.
By using variational methods and some properties of the Nehari manifold,
we prove that the biharmonic elliptic problem has at least two nontrivial
solutions.
is a sign-changing weight function.
By using variational methods and some properties of the Nehari manifold,
we prove that the biharmonic elliptic problem has at least two nontrivial
solutions.
Submitted August 18, 2016. Published October 26, 2016.
Math Subject Classifications: 35J50, 35J60, 35J62, 35J96.
Key Words: Biharmonic elliptic problem; second Hessian; variational methods;
Nehari manifold.
Show me the PDF file (267 KB),
TEX file for this article.
 |
Fei Fang
Department of Mathematics
Beijing Technology and Business University
Beijing 100048, China
email: fangfei68@163.com
|
|---|
 |
Chao Ji
Department of Mathematics
East China University of Science and Technology
Shanghai 200237, China
email: jichao@ecust.edu.cn
|
|---|
 |
Binlin Zhang
Department of Mathematics
Heilongjiang Institute of Technology
Harbin 150050, China
email: zhangbinlin2012@163.com
|
|---|
Return to the EJDE web page
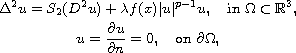
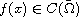 is a sign-changing weight function.
By using variational methods and some properties of the Nehari manifold,
we prove that the biharmonic elliptic problem has at least two nontrivial
solutions.
is a sign-changing weight function.
By using variational methods and some properties of the Nehari manifold,
we prove that the biharmonic elliptic problem has at least two nontrivial
solutions.


