Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 92, pp. 1-16.
Bifurcation for elliptic forth-order
problems with quasilinear source term
Soumaya Saanouni, Nihed Trabelsi
Abstract:
We study the bifurcations of the semilinear elliptic forth-order
problem with Navier boundary conditions
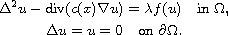
Where
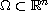 ,
,
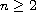 is a smooth bounded
domain, f is a positive, increasing and convex source term and
is a smooth bounded
domain, f is a positive, increasing and convex source term and
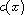 is a smooth positive function on
is a smooth positive function on
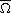 such
that the
such
that the
 -norm
of its gradient is small enough. We prove
the existence, uniqueness and stability of positive solutions. We
also show the existence of critical value
-norm
of its gradient is small enough. We prove
the existence, uniqueness and stability of positive solutions. We
also show the existence of critical value
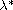 and the uniqueness of its extremal solutions.
and the uniqueness of its extremal solutions.
Submitted December 3 2015. Published April 6, 2016.
Math Subject Classifications: 35B32, 35B65, 35B35, 35J62.
Key Words: Bifurcation; regularity; stability; quasilinear.
Show me the PDF file (291 KB),
TEX file for this article.
 |
Soumaya Sâanouni
University of Tunis El Manar
Faculty of Sciences of Tunis
Department of Mathematics
Campus University 2092 Tunis, Tunisia
email: saanouni.soumaya@yahoo.com
|
|---|
 |
Nihed Trabelsi
University of Tunis El Manar
Higher Institute of Medical Technologies of Tunis
9 Street Dr. Zouhair Essafi 1006 Tunis, Tunisia
email: nihed.trabelsi78@gmail.com
|
|---|
Return to the EJDE web page
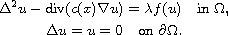
 ,
,
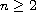 is a smooth bounded
domain, f is a positive, increasing and convex source term and
is a smooth bounded
domain, f is a positive, increasing and convex source term and
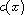 is a smooth positive function on
is a smooth positive function on
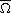 such
that the
such
that the
 -norm
of its gradient is small enough. We prove
the existence, uniqueness and stability of positive solutions. We
also show the existence of critical value
-norm
of its gradient is small enough. We prove
the existence, uniqueness and stability of positive solutions. We
also show the existence of critical value
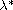 and the uniqueness of its extremal solutions.
and the uniqueness of its extremal solutions.

