We show that for each
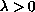 ,
the problem
,
the problem 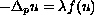 in
in
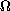 ,
, 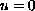 on
on
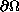
has a sequence of positive solutions
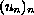 with
with
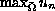 decreasing to zero. We assume that
decreasing to zero. We assume that
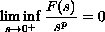 and that
and that
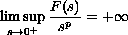 ,
where
,
where
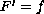 .
We stress that no condition on the sign of
.
We stress that no condition on the sign of
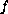 is imposed.
is imposed.
Pierpaolo Omari & Fabio Zanolin
Abstract:
We show that for each
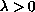 ,
the problem
,
the problem
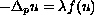 in
in
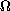 ,
,
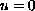 on
on
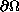
has a sequence of positive solutions
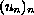 with
with
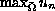 decreasing to zero. We assume that
decreasing to zero. We assume that
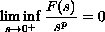 and that
and that
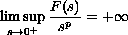 ,
where
,
where
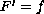 .
We stress that no condition on the sign of
.
We stress that no condition on the sign of
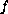 is imposed.
is imposed.
Published October 13, 2000.
Math Subject Classifications: 35J65, 34B15, 34C25, 47H15.
Key Words: Quasilinear elliptic equation, positive solution,
upper and lower solutions, time-mapping estimates.
Show me the PDF file (124K), TEX file, and other files for this article.
Fabio Zanolin
Dipartimento di Matematica e Informatica
Universita, Via delle Scienze 206
I--33100 Udine, Italy
e-mail: zanolin@dimi.uniud.it