Electron. J. Diff. Eqns.,
Vol. 1994(1994), No. 04, pp. 1-10.
Existence results for non-autonomous elliptic boundary value problems
V. Anuradha, S. Dickens, & R. Shivaji
Abstract:
We study solutions to the boundary value problems
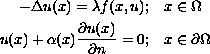
where
 ,
,
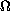 is a bounded region in
is a bounded region in
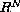 ;
;
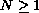 with smooth boundary
with smooth boundary
 ,
,
 , n is the outward unit normal, and f is
a smooth function such that it has either sublinear or restricted
linear growth in u at infinity, uniformly in x.
We also consider f such that
, n is the outward unit normal, and f is
a smooth function such that it has either sublinear or restricted
linear growth in u at infinity, uniformly in x.
We also consider f such that
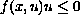 uniformly in
x, when |u| is large. Without requiring any sign condition
on
uniformly in
x, when |u| is large. Without requiring any sign condition
on
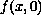 , thus allowing for both positone as well as
semipositone structure, we discuss the existence of at least
three solutions for given
, thus allowing for both positone as well as
semipositone structure, we discuss the existence of at least
three solutions for given
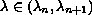 where
where
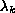 is the k-th eigenvalue of
is the k-th eigenvalue of
 subject
to the above boundary conditions.
In particular, one of the solutions we obtain has non-zero
positive part, while another has non-zero negative part.
We also discuss the existence of three solutions where one of
them is positive, while another is negative, for
subject
to the above boundary conditions.
In particular, one of the solutions we obtain has non-zero
positive part, while another has non-zero negative part.
We also discuss the existence of three solutions where one of
them is positive, while another is negative, for
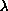 near
near
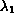 , and for
, and for
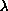 large when f is sublinear. We use the method of sub-super
solutions to establish our existence results. We further
discuss non-existence results for
large when f is sublinear. We use the method of sub-super
solutions to establish our existence results. We further
discuss non-existence results for
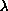 small.
small.
Submitted January 23, 1994. Published July 8, 1994.
Math Subject Classification: 35J65.
Key Words: Elliptic boundary value problems, semipositone.
Show me the
PDF(154K),
TEX file for this article.
|
V. Anuradha
Department of Mathematics and Statistics
University of Arkansas at Little Rock
Little Rock, AR 72204-1099, USA |
|
S. Dickens
Department of Mathematics and Statistics
Mississippi State University
Mississippi State, MS 39762, USA |
 |
R. Shivaji
Department of Mathematics and Statistics
Mississippi State University
Mississippi State, MS 39762, USA
e-mail: shivaji@math.msstate.edu |
Return to the EJDE home page.
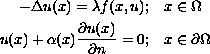
 ,
,
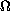 is a bounded region in
is a bounded region in
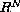 ;
;
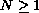 with smooth boundary
with smooth boundary
 ,
,
 ,
, 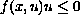 uniformly in
uniformly in
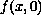 , thus allowing for both positone as well as
semipositone structure, we discuss the existence of at least
three solutions for given
, thus allowing for both positone as well as
semipositone structure, we discuss the existence of at least
three solutions for given
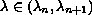 where
where
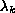 is the
is the  subject
to the above boundary conditions.
In particular, one of the solutions we obtain has non-zero
positive part, while another has non-zero negative part.
We also discuss the existence of three solutions where one of
them is positive, while another is negative, for
subject
to the above boundary conditions.
In particular, one of the solutions we obtain has non-zero
positive part, while another has non-zero negative part.
We also discuss the existence of three solutions where one of
them is positive, while another is negative, for
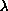 near
near
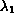 , and for
, and for
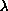 large when
large when 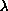 small.
small.
