In this paper we study for small positive
the slow motion of the solution
for evolution equations of Burgers' type with small diffusion,
,
,
(
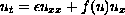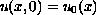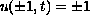)on the bounded spatial domain [-1,1];
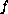is a smooth
function satisfying
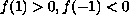and
.
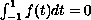The initial and boundary value problem
() has a unique
asymptotically stable equilibrium solution that attracts
all solutions starting with continuous initial data
.
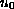On the infinite spatial domain
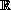the
differential
equation has slow speed traveling wave solutions generated by profiles
that satisfy the boundary conditions of
().
As long as its zero stays inside the interval [-1,1],
such a traveling wave suitably describes the slow long term behaviour
of the solution of
()
and its speed characterizes the local velocity
of the slow motion with exponential precision.
A solution that starts near a traveling wave moves in a small
neighborhood of the traveling wave with exponentially slow
velocity (measured as the speed of the unique zero)
during an exponentially long time interval (0,T).
In this paper we give a unified treatment of the problem, using both Hilbert
space and maximum principle methods, and we give
rigorous proofs of convergence of the solution and of the
asymptotic estimate of the velocity.