Electron. J. Diff. Eqns., Vol. 2002(2002), No. 33, pp. 1-12.
On the eigenvalue problem for the Hardy-Sobolev operator
with indefinite weights
K. Sreenadh
Abstract:
In this paper we study the eigenvalue problem
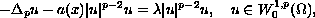
where
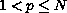 ,
,
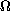 is a bounded domain containing 0 in
is a bounded domain containing 0 in
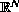 ,
,
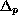 is the p-Laplacean, and
is the p-Laplacean, and
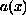 is a function related to Hardy-Sobolev inequality.
The weight function
is a function related to Hardy-Sobolev inequality.
The weight function
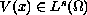 may change sign
and has nontrivial positive part. We study the simplicity,
isolatedness of the first eigenvalue, nodal domain properties.
Furthermore we show the existence of a nontrivial curve in the
Fucik spectrum.
may change sign
and has nontrivial positive part. We study the simplicity,
isolatedness of the first eigenvalue, nodal domain properties.
Furthermore we show the existence of a nontrivial curve in the
Fucik spectrum.
Submitted October 23, 2001. Published April 2, 2002.
Math Subject Classifications: 35J20, 35J70, 35P05, 35P30.
Key Words: p-Laplcean, Hardy-Sobolev operator, Fucik spectrum,
Indefinite weight.
Show me the
PDF file (275K),
TEX file for this article.
 |
Konijeti Sreenadh
Department of Mathematics
Indian Institute of Technology
Kanpur 208016, India.
e-mail: snadh@iitk.ac.in |
|---|
Return to the EJDE web page
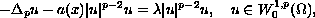
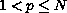 ,
,
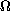 is a bounded domain containing 0 in
is a bounded domain containing 0 in
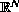 ,
,
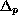 is the p-Laplacean, and
is the p-Laplacean, and
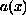 is a function related to Hardy-Sobolev inequality.
The weight function
is a function related to Hardy-Sobolev inequality.
The weight function
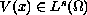 may change sign
and has nontrivial positive part. We study the simplicity,
isolatedness of the first eigenvalue, nodal domain properties.
Furthermore we show the existence of a nontrivial curve in the
Fucik spectrum.
may change sign
and has nontrivial positive part. We study the simplicity,
isolatedness of the first eigenvalue, nodal domain properties.
Furthermore we show the existence of a nontrivial curve in the
Fucik spectrum.
