Electron. J. Diff. Eqns., Vol. 2002(2002), No. 44, pp. 1-14.
Exponential decay for the solution of semilinear viscoelastic wave
equations with localized damping
Marcelo M. Cavalcanti,
Valeria N. Domingos Cavalcanti, &
Juan A. Soriano
Abstract:
In this paper we obtain an exponential rate of decay for
the solution of the viscoelastic nonlinear wave equation
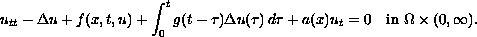
Here the damping term
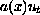 may be null for some part of the domain
may be null for some part of the domain
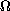 .
By assuming that the kernel
.
By assuming that the kernel
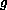 in the memory term decays exponentially, the damping effect allows
us to avoid compactness arguments and and to reduce number of
the energy estimates considered in the prior literature. We
construct a suitable Liapunov functional and make use of
the perturbed energy method.
in the memory term decays exponentially, the damping effect allows
us to avoid compactness arguments and and to reduce number of
the energy estimates considered in the prior literature. We
construct a suitable Liapunov functional and make use of
the perturbed energy method.
Submitted March 07, 2002. Published May 22, 2002.
Math Subject Classifications: 35L05, 35L70, 35B40, 74D10.
Key Words: semilinear wave equation, memory, localized damping.
Show me the
PDF file (264K),
TEX file for this article.
 |
Marcelo M. Cavalcanti
Universidade Estadual de Maringa,
87020-900 Maringa-PR, Brazil
e-mail: marcelo@gauss.dma.uem.br
|
|---|
 |
Valeria N. Domingos Cavalcanti
Universidade Estadual de Maringa,
87020-900 Maringa-PR, Brazil
e-mail: valeria@gauss.dma.uem.br
|
|---|
 |
Juan Amadeo Soraino
Universidade Estadual de Maringa,
87020-900 Maringa-PR, Brazil
e-mail: soriano@gauss.dma.uem.br
|
|---|
Return to the EJDE web page
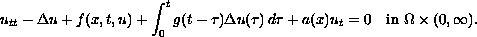
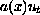 may be null for some part of the domain
may be null for some part of the domain
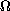 .
By assuming that the kernel
.
By assuming that the kernel
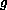 in the memory term decays exponentially, the damping effect allows
us to avoid compactness arguments and and to reduce number of
the energy estimates considered in the prior literature. We
construct a suitable Liapunov functional and make use of
the perturbed energy method.
in the memory term decays exponentially, the damping effect allows
us to avoid compactness arguments and and to reduce number of
the energy estimates considered in the prior literature. We
construct a suitable Liapunov functional and make use of
the perturbed energy method.


