Electron. J. Diff. Eqns., Vol. 2002(2002), No. 75, pp. 1-11.
Regularity bounds on Zakharov system evolutions
James Colliander & Gigliola Staffilani
Abstract:
Spatial regularity properties of certain global-in-time
solutions of the Zakharov system are established.
In particular, the evolving solution
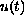 is shown to
satisfy an estimate
is shown to
satisfy an estimate
 ,
where
,
where
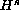 is the standard spatial Sobolev norm. The proof
is an adaptation of earlier work on the nonlinear Schrodinger
equation which reduces matters to bilinear estimates.
is the standard spatial Sobolev norm. The proof
is an adaptation of earlier work on the nonlinear Schrodinger
equation which reduces matters to bilinear estimates.
Submitted March 15, 2002. Published August 20, 2002.
Math Subject Classifications: 35Q55.
Key Words: initial value problems, bilinear estimates,
Zakharov system, weak turbulence.
Show me the
PDF file (264K),
TEX file for this article.
|
James Colliander
Department of Mathematics
University of Toronto
Toronto, ON M5R 1W8 Canada
e-mail: colliand@math.toronto.edu |
|---|
 |
Gigliola Staffilani
Department of Mathematics
Massachusets Institute of Technology
77 Massachusets Avenue
Cambridge, MA 02139-4307 USA
e-mail: gigliola@math.mit.edu |
|---|
Return to the EJDE web page
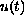 is shown to
satisfy an estimate
is shown to
satisfy an estimate
 ,
where
,
where
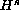 is the standard spatial Sobolev norm. The proof
is an adaptation of earlier work on the nonlinear Schrodinger
equation which reduces matters to bilinear estimates.
is the standard spatial Sobolev norm. The proof
is an adaptation of earlier work on the nonlinear Schrodinger
equation which reduces matters to bilinear estimates.
