Electron. J. Diff. Eqns., Vol. 2002(2002), No. 97, pp. 1-19.
Nonexistence of solutions to systems of higher-order semilinear
inequalities in cone-like domains
Abdallah El Hamidi & Gennady G. Laptev
Abstract:
In this paper, we obtain nonexistence results for global
solutions to the system of higher-order semilinear partial
differential inequalities

in cones and cone-like domains in
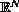 ,
,
 .
Our results apply to nonnegative solutions
and to solutions which change sign. Moreover, we provide
a general formula of the critical exponent corresponding to
this system. Our proofs are based on the test function method,
developed by Mitidieri and Pohozaev.
.
Our results apply to nonnegative solutions
and to solutions which change sign. Moreover, we provide
a general formula of the critical exponent corresponding to
this system. Our proofs are based on the test function method,
developed by Mitidieri and Pohozaev.
Submitted March 10, 2002. Published November 14, 2002.
Math Subject Classifications: 35G25, 35R45.
Key Words: nonexistence, blow-up, higher-order differential
inequalities, critical exponent.
Show me the
PDF file (305K),
TEX file for this article.
 |
Abdallah El hamidi
Laboratoire de Mathematiques
Universite de La Rochelle
Avenue Michel Crepeau
17000 La Rochelle, France
e-mail: aelhamid@univ-lr.fr
|
|---|
 |
Gennady G. Laptev
Department of Function Theory
Steklov Mathematical Institute
Gubkina 8, 117966 Moscow, Russia
e-mail: laptev@home.tula.net
|
|---|
Return to the EJDE web page

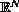 ,
,
 .
Our results apply to nonnegative solutions
and to solutions which change sign. Moreover, we provide
a general formula of the critical exponent corresponding to
this system. Our proofs are based on the test function method,
developed by Mitidieri and Pohozaev.
.
Our results apply to nonnegative solutions
and to solutions which change sign. Moreover, we provide
a general formula of the critical exponent corresponding to
this system. Our proofs are based on the test function method,
developed by Mitidieri and Pohozaev.

