A double fixed point theorem is applied to yield the existence of at least two nonnegative solutions for the three-point boundary-value problem for a second-order differential equation,

where
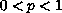 is fixed, and
is fixed, and
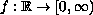 is
continuous.
is
continuous.
Johnny Henderson
Abstract:
A double fixed point theorem is applied to yield the
existence of at least two nonnegative solutions for the three-point
boundary-value problem for a second-order differential equation,

where
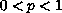 is fixed, and
is fixed, and
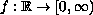 is
continuous.
is
continuous.
Submitted September 16, 2003. Published October 5, 2004.
Math Subject Classifications: 34B15, 34B10, 34B18.
Key Words: Fixed point theorem; three-point; boundary-value problem.
Show me the PDF file (192K), TEX file for this article.
 |
Johnny Henderson Department of Mathematics Baylor University Waco, TX 76798-7328, USA email: Johnny_Henderson@baylor.edu |
|---|
Return to the EJDE web page