Electron. J. Diff. Eqns., Vol. 2004(2004), No. 91, pp. 1-7.
Solution matching for a three-point boundary-value
problem on atime scale
Martin Eggensperger, Eric R. Kaufmann, Nickolai Kosmatov
Abstract:
Let
 be a time scale such that
be a time scale such that
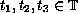 .
We show the existence of a unique solution for the three-point boundary
value problem
.
We show the existence of a unique solution for the three-point boundary
value problem
![$$\displaylines{
y^{\Delta\Delta\Delta}(t) = f(t, y(t), y^\Delta(t),
y^{\Delta\Delta}(t)), \quad t \in [t_1, t_3] \cap \mathbb{T},\cr
y(t_1) = y_1, \quad y(t_2) = y_2, \quad y(t_3) = y_3\,.
}$$](gifs/ac.gif)
We do this by matching a solution to the first equation satisfying a
two-point boundary conditions on
![$[t_1, t_2] \cap \mathbb{T}$](gifs/ad.gif) with a solution satisfying a two-point boundary conditions on
with a solution satisfying a two-point boundary conditions on
![$[t_2, t_3] \cap \mathbb{T}$](gifs/ae.gif) .
.
Submitted May 14, 2004. Published July 8, 2004.
Math Subject Classifications: 34B10, 34B15, 34G20.
Key Words: Time scale; boundary-value problem; solution matching.
Show me the
PDF file (206K),
TEX file for this article.
| |
Martin Eggensperger
General Studies, Southeast Arkansas College
Pine Bluff, Arkansas, USA
email: meggensperger@seark.edu |
|---|
 |
Eric R. Kaufmann
Department of Mathematics and Statistics
University of Arkansas at Little Rock
Little Rock, Arkansas 72204-1099, USA
email: erkaufmann@ualr.edu
|
|---|
| |
Nickolai Kosmatov
Department of Mathematics and Statistics
University of Arkansas at Little Rock
Little Rock, Arkansas 72204-1099, USA
email: nxkosmatov@ualr.edu
|
|---|
Return to the EJDE web page
 be a time scale such that
be a time scale such that
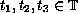 .
We show the existence of a unique solution for the three-point boundary
value problem
.
We show the existence of a unique solution for the three-point boundary
value problem
![$$\displaylines{
y^{\Delta\Delta\Delta}(t) = f(t, y(t), y^\Delta(t),
y^{\Delta\Delta}(t)), \quad t \in [t_1, t_3] \cap \mathbb{T},\cr
y(t_1) = y_1, \quad y(t_2) = y_2, \quad y(t_3) = y_3\,.
}$$](gifs/ac.gif)
![$[t_1, t_2] \cap \mathbb{T}$](gifs/ad.gif) with a solution satisfying a two-point boundary conditions on
with a solution satisfying a two-point boundary conditions on
![$[t_2, t_3] \cap \mathbb{T}$](gifs/ae.gif) .
.
