Electron. J. Diff. Eqns.,
Vol. 2005(2005), No. 106, pp. 1-18.
Positive solutions of three-point boundary-value problems
for p-Laplacian singular differential equations
George N. Galanis, Alex P. Palamides
Abstract:
In this paper we prove the existence of positive solutions for the
three-point singular boundary-value problem
![$$
-[\phi _{p}(u')]'=q(t)f(t,u(t)),\quad 0<t<1
$$](gifs/aa.gif)
subject to
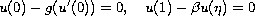
or to
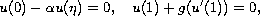
where
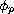 is the
is the
 -Laplacian operator,
-Laplacian operator,
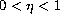 ;
;
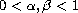 are fixed points and
are fixed points and
 is a monotone
continuous function defined on the real line
is a monotone
continuous function defined on the real line
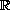 with
with
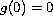 and
and
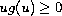 .
Our approach is a combination of
Nonlinear Alternative of Leray-Schauder with the properties
of the associated vector field at the
.
Our approach is a combination of
Nonlinear Alternative of Leray-Schauder with the properties
of the associated vector field at the
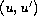 plane.
More precisely, we show that the solutions of the above
boundary-value problem remains away from the origin for
the case where the nonlinearity is sublinear and so we avoid
its singularity at
plane.
More precisely, we show that the solutions of the above
boundary-value problem remains away from the origin for
the case where the nonlinearity is sublinear and so we avoid
its singularity at
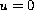 .
.
Submitted May 13, 2005. Published October 7, 2005.
Math Subject Classifications: 34B15, 34B18.
Key Words: Three-point singular boundary-value problem; p-Laplacian;
positive and negative solutions; vector field;
Nonlinear alternative of Leray-Schauder.
Show me the
PDF file (292K),
TEX file for this article.
 |
George N. Galanis
Naval Academy of Greece
Piraeus, 185 39, Greece
email: ggalanis@math.uoa.gr |
|---|
 |
Alex P. Palamides
Department of Communication Sciences
University of Peloponnese
22100 Tripolis, Greece
email: palamid@uop.gr |
|---|
Return to the EJDE web page
![$$
-[\phi _{p}(u')]'=q(t)f(t,u(t)),\quad 0<t<1
$$](gifs/aa.gif)
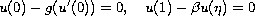
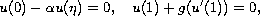
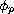 is the
is the
 -Laplacian operator,
-Laplacian operator,
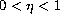 ;
;
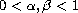 are fixed points and
are fixed points and
 is a monotone
continuous function defined on the real line
is a monotone
continuous function defined on the real line
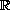 with
with
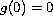 and
and
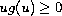 .
Our approach is a combination of
Nonlinear Alternative of Leray-Schauder with the properties
of the associated vector field at the
.
Our approach is a combination of
Nonlinear Alternative of Leray-Schauder with the properties
of the associated vector field at the
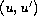 plane.
More precisely, we show that the solutions of the above
boundary-value problem remains away from the origin for
the case where the nonlinearity is sublinear and so we avoid
its singularity at
plane.
More precisely, we show that the solutions of the above
boundary-value problem remains away from the origin for
the case where the nonlinearity is sublinear and so we avoid
its singularity at
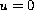 .
.

