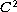 infinity-harmonic functions
infinity-harmonic functions
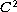 infinity-harmonic functions
infinity-harmonic functions
Yifeng Yu
Abstract:
In this paper, we prove that any nonconstant,
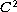 solution of the infinity Laplacian equation
solution of the infinity Laplacian equation
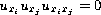 can not have interior critical points. This result was first
proved by Aronsson [2] in two dimensions. When the solution
is
can not have interior critical points. This result was first
proved by Aronsson [2] in two dimensions. When the solution
is
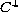 ,
Evans [6] established a Harnack inequality
for
,
Evans [6] established a Harnack inequality
for
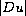 ,
which implies that non-constant
,
which implies that non-constant
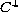 solutions
have no interior critical points for any dimension.
Our method is strongly motivated by the work in [6].
solutions
have no interior critical points for any dimension.
Our method is strongly motivated by the work in [6].
Submitted June 15, 2006. Published October 6, 2006.
Math Subject Classifications: 35B38.
Key Words: Infinity Laplacian equation; infinity harmonic function;
viscosity solutions.
Show me the PDF file (170K), TEX file for this article.
 |
Yifeng Yu Department of Mathematics University of Texas Austin, TX 78712, USA email: yifengyu@math.utexas.edu |
|---|
Return to the EJDE web page