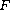 -harmonic maps
with finite
-harmonic maps
with finite
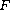 -energy
-energy
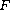 -harmonic maps
with finite
-harmonic maps
with finite
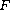 -energy
-energy
M'hamed Kassi
Abstract:
Let
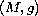 be a
be a
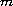 -dimensional
complete Riemannian manifold with a
pole, and
-dimensional
complete Riemannian manifold with a
pole, and
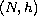 a Riemannian manifold. Let
a Riemannian manifold. Let
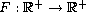 be a strictly increasing
be a strictly increasing
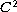 function such that
function such that
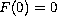 and
and
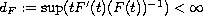 .
We show that if
.
We show that if
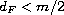 , then every
, then every
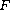 -harmonic
map
-harmonic
map
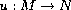 with finite
with finite
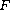 -energy
(i.e a local extremal of
-energy
(i.e a local extremal of
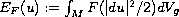 and
and
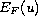 is finite) is a constant map provided that the radial curvature of
is finite) is a constant map provided that the radial curvature of
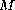 satisfies a pinching condition depending to
satisfies a pinching condition depending to
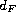 .
.
Submitted March 24, 2005. Published January 31, 2006.
Math Subject Classifications: 58E20, 53C21, 58J05.
Key Words: F-harmonic maps; Liouville propriety; Stokes formula;
comparison theorem.
Show me the PDF file (212K), TEX file for this article.
 |
M'hamed Kassi Equipe d'Analyse Complexe, Laboratoire d'Analyse Fonctionnelle Harmonique et Complexe Département de Mathématiques, Faculté des Sciences Université Ibn Tofail, Kénitra, Maroc email: mhamedkassi@yahoo.fr |
|---|
Return to the EJDE web page