Electron. J. Diff. Eqns., Vol. 2006(2006), No. 37, pp. 1-7.

Multiple solutions for the $p$-Laplace equation with nonlinear boundary conditions

Julian Fernandez Bonder

Abstract:
In this note, we show the existence of at least three nontrivial solutions to the quasilinear elliptic equation
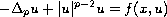
$$ -\Delta_p u + |u|^{p-2}u = f(x,u) $$
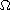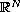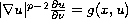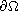in a smooth bounded domain $\Omega$ of $\mathbb{R}^N$ with nonlinear boundary conditions $|\nabla u|^{p-2}\frac{\partial u}{\partial\nu} = g(x,u)$ on $\partial\Omega$. The proof is based on variational arguments.

Submitted January 10, 2006. Published March 21, 2006.
Math Subject Classifications: 35J65, 35J20.
Key Words: p-Laplace equations; nonlinear boundary conditions; variational methods.

Show me the PDF file (209K), TEX file, and other files for this article.

Julián Fernández Bonder
Departamento de Matemática, FCEyN
UBA (1428) Buenos Aires, Argentina
email: jfbonder@dm.uba.ar
http://mate.dm.uba.ar/~jfbonder

Return to the EJDE web page