Eada A. El-Zahrani, Hassan M. Serag
Abstract:
In this paper, we consider the nonlinear elliptic system
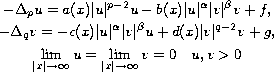
on a bounded and unbounded domains of
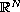 ,
where
,
where
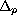 denotes the p-Laplacian.
The existence of weak solutions for these systems is proved using
the theory of monotone operators
denotes the p-Laplacian.
The existence of weak solutions for these systems is proved using
the theory of monotone operators
Submitted February 9, 2006. Published July 6, 2006.
Math Subject Classifications: 35B45, 35J55.
Key Words: Weak solutions; nonlinear elliptic systems; p-Laplacian;
monotone operators.
Show me the PDF file (226K), TEX file for this article.
| Eada A. El-Zahrani Mathematics Department, Faculty of Science for Girls Dammam, P. O. Box 838, Pincode 31113, Saudi Arabia | |
 |
Hassan M. Serag Mathematics Department Faculty of Science, Al-Azhar University Nasr City (11884), Cairo, Egypt email: serraghm@yahoo.com |
Return to the EJDE web page