Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 71, pp. 1-17.
Energy quantization for Yamabe's problem in conformal dimension
Fethi Mahmoudi
Abstract:
Riviere [11] proved an energy quantization for
Yang-Mills fields defined on
 -dimensional Riemannian manifolds,
when
-dimensional Riemannian manifolds,
when
 is larger than the critical dimension 4. More precisely,
he proved that the defect measure of a weakly converging sequence
of Yang-Mills fields is quantized, provided the
is larger than the critical dimension 4. More precisely,
he proved that the defect measure of a weakly converging sequence
of Yang-Mills fields is quantized, provided the
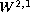 norm
of their curvature is uniformly bounded. In the present paper,
we prove a similar quantization phenomenon for the nonlinear
elliptic equation
norm
of their curvature is uniformly bounded. In the present paper,
we prove a similar quantization phenomenon for the nonlinear
elliptic equation
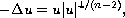
in a subset
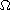 of
of
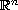 .
.
Submitted February 20, 2006. Published July 7, 2006.
Math Subject Classifications: 35B33, 46E30, 46L65.
Key Words: Critical exponents; Lorentz spaces; quantization phenomena.
Show me the
PDF file (277K),
TEX file for this article.
 |
Fethi Mahmoudi
Scuola Internazionale Superiore Di Studi Avanzati (Sissa)
Via Beirut 2-4, 34014 Trieste, Italy
email: mahmoudi@sissa.it |
|---|
Return to the EJDE web page
 -dimensional Riemannian manifolds,
when
-dimensional Riemannian manifolds,
when
 is larger than the critical dimension 4. More precisely,
he proved that the defect measure of a weakly converging sequence
of Yang-Mills fields is quantized, provided the
is larger than the critical dimension 4. More precisely,
he proved that the defect measure of a weakly converging sequence
of Yang-Mills fields is quantized, provided the
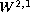 norm
of their curvature is uniformly bounded. In the present paper,
we prove a similar quantization phenomenon for the nonlinear
elliptic equation
norm
of their curvature is uniformly bounded. In the present paper,
we prove a similar quantization phenomenon for the nonlinear
elliptic equation
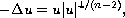
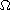 of
of
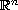 .
.
