Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 142, pp. 1-9.
Ambarzumian's theorem for trees
Robert Carlson, Vyacheslav Pivovarchik
Abstract:
The classical Ambarzumian's Theorem for Schrodinger operators
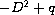 on an interval, with Neumann conditions at the endpoints,
says that if the spectrum of
on an interval, with Neumann conditions at the endpoints,
says that if the spectrum of
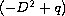 is the same as the spectrum of
is the same as the spectrum of
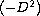 then
then
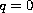 .
This theorem is generalized to Schrodinger operators
on metric trees with Neumann conditions at the boundary vertices.
.
This theorem is generalized to Schrodinger operators
on metric trees with Neumann conditions at the boundary vertices.
Submitted April 12, 2007. Published October 24, 2007.
Math Subject Classifications: 34B45.
Key Words: Inverse eigenvalue problem; quantum graph.
Show me the
PDF file (205 KB),
TEX file for this article.
 |
Robert Carlson
University of Colorado at Colorado Springs
Colorado Springs, CO 80933, USA
e-mail: carlson@uccs.edu |
 |
Vyacheslav Pivovarchik
South-Ukrainian State Pedagogical University
Staroportofrankovskaya Ul. 26, 65020 Odessa, Ukraine
email: v.pivovarchik@paco.net vnp.@dtp.odessa.ua
|
|---|
Return to the EJDE web page
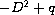 on an interval, with Neumann conditions at the endpoints,
says that if the spectrum of
on an interval, with Neumann conditions at the endpoints,
says that if the spectrum of
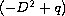 is the same as the spectrum of
is the same as the spectrum of
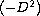 then
then
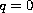 .
This theorem is generalized to Schrodinger operators
on metric trees with Neumann conditions at the boundary vertices.
.
This theorem is generalized to Schrodinger operators
on metric trees with Neumann conditions at the boundary vertices.

