We consider divergence form elliptic operators
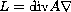 in
in
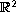 with a coefficient
matrix
with a coefficient
matrix
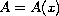 of bounded measurable functions independent of the
of bounded measurable functions independent of the
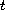 -direction.
The aim of this note is to demonstrate how the
proof of the main theorem in [4] can be modified to bounded
Lipschitz domains. The original theorem states that the
-direction.
The aim of this note is to demonstrate how the
proof of the main theorem in [4] can be modified to bounded
Lipschitz domains. The original theorem states that the
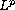 Neumann
and regularity problems are solvable for
Neumann
and regularity problems are solvable for
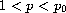 for some
for some
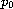 in domains of the form
in domains of the form
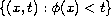 , where
, where
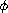 is a Lipschitz function. The exponent
is a Lipschitz function. The exponent
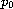 depends only on the
ellipticity constants and the Lipschitz constant of
depends only on the
ellipticity constants and the Lipschitz constant of
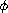 .
The principal modification of the argument for the original
result is to prove the boundedness of the layer potentials on domains
of the form
.
The principal modification of the argument for the original
result is to prove the boundedness of the layer potentials on domains
of the form
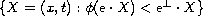 ,
for a fixed unit vector
,
for a fixed unit vector
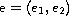 and
and
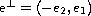 .
This is proved in [4] only in the case
.
This is proved in [4] only in the case
 .
A simple localisation argument then
completes the proof.
.
A simple localisation argument then
completes the proof.
