Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 56, pp. 1-21.
Boundary-value problems for second-order differential operators
with nonlocal boundary conditions
Mohamed Denche, Abderrahmane Meziani
Abstract:
In this paper, we study a second-order differential operator combining
weighting integral boundary condition with another two-point boundary
condition. Under certain conditions on the weighting functions, called
regular and non regular cases, we prove that the resolvent decreases with
respect to the spectral parameter in
 , but there is no maximal
decrease at infinity for
, but there is no maximal
decrease at infinity for
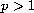 .
Furthermore, the studied operator generates
in
.
Furthermore, the studied operator generates
in
 ,
an analytic semi group for
,
an analytic semi group for
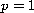 in the regular case, and
an analytic semi group with singularities for
in the regular case, and
an analytic semi group with singularities for
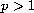 ,
in both cases, and for
,
in both cases, and for
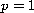 ,
in the non regular case only. The obtained results are then used to
show the correct solvability of a mixed problem for parabolic partial
differential equation with non regular boundary conditions.
,
in the non regular case only. The obtained results are then used to
show the correct solvability of a mixed problem for parabolic partial
differential equation with non regular boundary conditions.
Submitted May 10, 2006. Published April 17, 2007.
Math Subject Classifications: 47E05, 35K20.
Key Words: Green's function; regular and non regular boundary conditions;
semi group with singularities; weighted mixed boundary conditions.
Show me the
PDF file (295K),
TEX file for this article.
 |
Mohamed Denche
Laboratoire Equations Differentielles
Departement de Mathematiques
Faculte des Sciences, Universite Mentouri
25000 Constantine, Algeria
email: denech@wissal.dz |
|---|
 |
Abderrahmane Meziani
Laboratoire Equations Differentielles
Departement de Mathematiques
Faculte des Sciences, Universite Mentouri
25000 Constantine, Algeria
email: mezianiar@yahoo.fr |
|---|
Return to the EJDE web page
 , but there is no maximal
decrease at infinity for
, but there is no maximal
decrease at infinity for
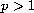 .
Furthermore, the studied operator generates
in
.
Furthermore, the studied operator generates
in
 ,
an analytic semi group for
,
an analytic semi group for
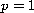 in the regular case, and
an analytic semi group with singularities for
in the regular case, and
an analytic semi group with singularities for
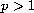 ,
in both cases, and for
,
in both cases, and for
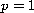 ,
in the non regular case only. The obtained results are then used to
show the correct solvability of a mixed problem for parabolic partial
differential equation with non regular boundary conditions.
,
in the non regular case only. The obtained results are then used to
show the correct solvability of a mixed problem for parabolic partial
differential equation with non regular boundary conditions.

