Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 69, pp. 1-9.
A fibering map approach to a semilinear elliptic boundary value problem
Kenneth J. Brown, Tsung-Fang Wu
Abstract:
We prove the existence of at least two positive solutions for
the semilinear elliptic boundary-value problem
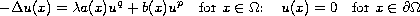
on a bounded region
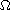 by using the Nehari manifold and
the fibering maps associated with the Euler functional for the problem.
We show how knowledge of the fibering maps for the problem leads to
very easy existence proofs.
by using the Nehari manifold and
the fibering maps associated with the Euler functional for the problem.
We show how knowledge of the fibering maps for the problem leads to
very easy existence proofs.
Submitted February 27, 2007. Published May 10, 2007.
Math Subject Classifications: 35J20, 36J65.
Key Words: Semilinear elliptic boundary value problem;
variational methods; Nehari manifold; fibering map.
Show me the
PDF file (216K),
TEX file for this article.
 |
Kenneth J. Brown
School of Mathematical and Computer Sciences
and the Maxwell Institute, Heriot-Watt University
Riccarton, Edinburgh EH14 4AS, UK
email: K.J.Brown@hw.ac.uk |
|---|
 |
Tsung-Fang Wu
Department of Applied Mathematics
National University of Kaohsiung
Kaohsiung 811, Taiwan
email: tfwu@nuk.edu.tw |
|---|
Return to the EJDE web page
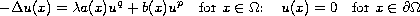
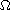 by using the Nehari manifold and
the fibering maps associated with the Euler functional for the problem.
We show how knowledge of the fibering maps for the problem leads to
very easy existence proofs.
by using the Nehari manifold and
the fibering maps associated with the Euler functional for the problem.
We show how knowledge of the fibering maps for the problem leads to
very easy existence proofs.

