Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 148, pp. 1-6.
A note on radial nonlinear Schrodinger systems
with nonlinearity spatially modulated
Juan Belmonte-Beitia
Abstract:
First, we prove that for Schrodinger radial systems
the polar angular coordinate must satisfy
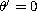 .
Then using radial symmetry, we transform the system
into a generalized Ermakov-Pinney equation and prove the existence
of positive periodic solutions.
.
Then using radial symmetry, we transform the system
into a generalized Ermakov-Pinney equation and prove the existence
of positive periodic solutions.
Submitted May 13, 2008. Published October 29, 2008.
Math Subject Classifications: 35Q55, 34B15, 35Q51.
Key Words: Nonlinear Schrodinger equation; nonlinearity spatially modulated;
Ermakov-Pinney equation; fixed point theorem.
Show me the
PDF file (195 KB),
TEX file for this article.
 |
Juan Belmonte-Beitia
Departamento de Matemáticas,
E. T. S. de Ingenieros Industriales
and Instituto de Matemática Aplicada a la Ciencia y la Ingeniería
(IMACI)
Universidad de Castilla-La Mancha s/n, 13071 Ciudad Real, Spain
email: juan.belmonte@uclm.es
|
|---|
Return to the EJDE web page
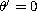 .
Then using radial symmetry, we transform the system
into a generalized Ermakov-Pinney equation and prove the existence
of positive periodic solutions.
.
Then using radial symmetry, we transform the system
into a generalized Ermakov-Pinney equation and prove the existence
of positive periodic solutions.
