Electron. J. Diff. Eqns., Vol. 2009(2009), No. 32, pp. 1-10.

Existence of multiple solutions for a nonlinearly perturbed elliptic parabolic system in $\mathbb{R}^2$

Michinori Ishiwata, Takayoshi Ogawa, Futoshi Takahashi

Abstract:
We consider the following nonlinearly perturbed version of the elliptic-parabolic system of Keller-Segel type:
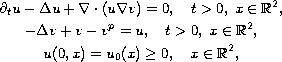
$$\displaylines{ \partial_tu - \Delta u+ \nabla \cdot(u \nabla v)=0,\quad t>0,\; x\in\mathbb{R}^2, \cr -\Delta v+v-v^p=u,\quad t>0,\; x\in\mathbb{R}^2,\cr u(0,x) =u_0(x)\ge 0,\quad x\in\mathbb{R}^2, }$$
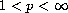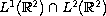where $1<p<\infty$. It has already been shown that the system admits a positive solution for a small nonnegative initial data in $L^1(\mathbb{R}^2)\cap L^2(\mathbb{R}^2)$ which corresponds to the local minimum of the associated energy functional to the elliptic part of the system. In this paper, we show that for a radially symmetric nonnegative initial data, there exists another positive solution which corresponds to the critical point of mountain-pass type. 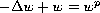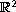The $v$-component of the solution bifurcates from the unique positive radially symmetric solution of $-\Delta w + w = w^p$ in $\mathbb{R}^2$.

Submitted August 22, 2008. Published February 16, 2009.
Math Subject Classifications: 35K15, 35K55, 35Q60, 78A35.
Key Words: Multiple existence; elliptic-parabolic system; unconditional uniqueness.

Show me the PDF file (250 KB), TEX file, and other files for this article.

Michinori Ishiwata
Common Subject Division, Muroran Institute of Technology
Muroran 050-8585, Japan
email: ishiwata@mmm.muroran-it.ac.jp
Takayoshi Ogawa
Mathematical Institute, Tohoku University
Sendai 980-8578, Japan
email: ogawa@math.tohoku.ac.jp
Futoshi Takahashi
Graduate School of Science, Osaka City University
Osaka 558-8585, Japan
email: futoshi@sci.osaka-cu.ac.jp

Return to the EJDE web page