Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 40, pp. 1-5.
A note on nodal non-radially symmetric solutions to
Emden-Fowler equations
Miguel Ramos, Wenming Zou
Abstract:
We prove the existence of an unbounded sequence of
sign-changing and non-radially symmetric solutions to the problem
 in
in
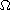 ,
,
 on
on
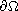 ,
,
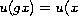 ),
),
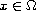 ,
,
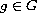 ,
where
,
where
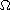 is
an annulus of
is
an annulus of
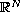 (
(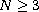 ),
),
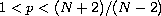 and
and
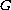 is a non-transitive closed subgroup of the orthogonal group
is a non-transitive closed subgroup of the orthogonal group
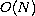 .
.
Submitted February 19, 2009. Published March 19, 2009.
Math Subject Classifications: 35J20, 35J25, 35B99.
Key Words: Emden-Fowler equation; nodal solutions; symmetric solutions;
variational methods.
Show me the PDF file (216 KB),
TEX file for this article.
Miguel Ramos
Universidade de Lisboa, CMAF-Faculty of Science
Av. Prof. Gama Pinto, 2, 1649-003-Lisboa, Portugal
email: mramos@ptmat.fc.ul.pt
|
Wenming Zou
Department of Mathematical Sciences, Tsinghua University
Beijing 100084, China
email: wzou@math.tsinghua.edu.cn
|
Return to the EJDE web page
 in
in
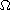 ,
,
 on
on
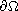 ,
,
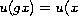 ),
),
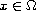 ,
,
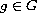 ,
where
,
where
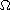 is
an annulus of
is
an annulus of
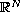 (
(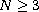 ),
),
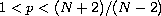 and
and
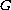 is a non-transitive closed subgroup of the orthogonal group
is a non-transitive closed subgroup of the orthogonal group
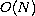 .
.