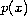 -Laplacian
non-homogeneous equations
-Laplacian
non-homogeneous equations
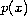 -Laplacian
non-homogeneous equations
-Laplacian
non-homogeneous equations
Ionica Andrei
Abstract:
We study the boundary value problem

where
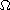 is a smooth bounded domain in
is a smooth bounded domain in
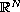 .
Our attention is focused on the cases when
.
Our attention is focused on the cases when
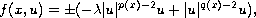
where
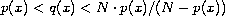 for
for
 in
in
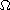 .
.
Submitted March 9, 2009. Published June 2, 2009.
Math Subject Classifications: 35D05, 35J60, 58E05
Key Words: p(x)-Laplace operator; generalized
Lebesgue-Sobolev space; critical point; weak solution.
Show me the PDF file (238 KB), TEX file for this article.
 |
Ionica Andrei Department of Mathematics, High School of Cujmir 227150 Cujmir, Romania email: andreiionica2003@yahoo.com |
|---|
Return to the EJDE web page