Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 88, pp. 1-7.
A class of generalized integral operators
Samir Bekkara, Bekkai Messirdi, Abderrahmane Senoussaoui
Abstract:
In this paper, we introduce a class of generalized integral
operators that includes Fourier integral operators.
We establish some conditions on these operators such that they
do not have bounded extension on
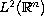 .
This permit us in particular to construct a class of Fourier
integral operators with bounded symbols in
.
This permit us in particular to construct a class of Fourier
integral operators with bounded symbols in
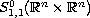 and in
and in
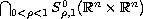 which cannot be extended to bounded operators in
which cannot be extended to bounded operators in
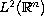 .
.
Submitted February 12, 2009. Published July 27, 2009.
Math Subject Classifications: 35S30, 35S05, 47A10, 35P05.
Key Words: Integral operators; L2-boundedness;
unbounded Fourier integral operators.
Show me the PDF file (225 KB),
TEX file for this article.
 |
Samir Bekkara
Université des Sciences et de la Technologie d'Oran
Faculté des Sciences, Département de Mathématiques,
Oran, Algeria
email: sbekkara@yahoo.fr
|
|---|
 |
Bekkai Messirdi, Abderrahmane Senoussaoui
Université d'Oran Es-Sénia, Faculté des Sciences
Département de Mathématiques. B.P. 1524 El-Mnaouer, Oran,
Algeria
email: bmessirdi@univ-oran.dz
|
|---|
 |
Abderrahmane Senoussaoui
Université d'Oran Es-Sénia, Faculté des Sciences
Département de Mathématiques. B.P. 1524 El-Mnaouer, Oran,
Algeria
email: senoussaoui.abdou@univ-oran.dz
|
|---|
Return to the EJDE web page
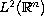 .
This permit us in particular to construct a class of Fourier
integral operators with bounded symbols in
.
This permit us in particular to construct a class of Fourier
integral operators with bounded symbols in
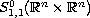 and in
and in
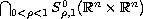 which cannot be extended to bounded operators in
which cannot be extended to bounded operators in
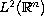 .
.


