Electron. J. Diff. Equ., Vol. 2010(2010), No. 171, pp. 1-8.

Positive solutions for singular Sturm-Liouville boundary value problems on the half line

Jiafa Xu, Zhilin Yang

Abstract:
This article concerns the existence and multiplicity of positive solutions for the singular Sturm-Liouville boundary value problem
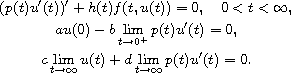
$$\displaylines{ (p(t)u'(t))'+h(t)f(t,u(t))=0,\quad 0<t<\infty,\cr au(0)-b\lim_{t\to 0^+}p(t)u'(t)=0,\cr c\lim_{t\to \infty}u(t)+d\lim_{t\to \infty}p(t)u'(t)=0. }$$
We use fixed point index theory to establish our main results based on a priori estimates derived by utilizing spectral properties of associated linear integral operators.

Submitted April 1, 2010. Published November 30, 2010.
Math Subject Classifications: 34B40, 34B16, 47H07, 47H11, 45M20.
Key Words: Sturm-Liouville problem on the half line; positive solution; fixed point index; spectral radius.

Show me the PDF file (202 KB), TEX file, and other files for this article.

Jiafa Xu
Department of Mathematics
Qingdao Technological University
Qingdao, Shandong Province, China
email: xujiafa292@sina.com
Zhilin Yang
Department of Mathematics
Qingdao Technological University
Qingdao, Shandong Province, China
email: zhilinyang@sina.com

Return to the EJDE web page