Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 105, pp. 1-8.
Existence of solutions for p-Kirchhoff
type problems with critical exponent
Ahmed Hamydy, Mohammed Massar, Najib Tsouli
Abstract:
We study the existence of solutions for the
p-Kirchhoff type problem involving the critical Sobolev
exponent,
![$$\displaylines{
-\Big[g\Big(\int_\Omega|\nabla u|^pdx\Big)\Big]\Delta_pu
=\lambda f(x,u)+|u|^{p^\star-2}u\quad\hbox{in }\Omega,\cr
u=0\quad\hbox{on }\partial\Omega,
}$$](gifs/aa.gif)
where
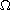 is a bounded smooth domain of
is a bounded smooth domain of
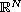 ,
,
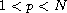 ,
,
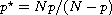 is the critical Sobolev
exponent,
is the critical Sobolev
exponent,
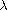 is a positive parameter, f and g are
continuous functions. The main results of this paper establish, via
the variational method. The concentration-compactness principle
allows to prove that the Palais-Smale condition is satisfied below a
certain level.
is a positive parameter, f and g are
continuous functions. The main results of this paper establish, via
the variational method. The concentration-compactness principle
allows to prove that the Palais-Smale condition is satisfied below a
certain level.
Submitted July 26, 2011. Published August 16, 2011.
Math Subject Classifications: 35A15, 35B33, 35J62.
Key Words: p-Kirchhoff; critical exponent; parameter; Lions principle.
Show me the PDF file (214 KB),
TEX file for this article.
 |
Ahmed Hamydy
University Mohamed I, Faculty of sciences
Department of Mathematics, Oujda, Morocco
email: a.hamydy@yahoo.fr
|
|---|
 |
Mohammed Massar
University Mohamed I, Faculty of sciences
Department of Mathematics, Oujda, Morocco
email: massarmed@hotmail.com
|
|---|
 |
Najib Tsouli
University Mohamed I, Faculty of sciences
Department of Mathematics, Oujda, Morocco
email: tsouli@hotmail.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
-\Big[g\Big(\int_\Omega|\nabla u|^pdx\Big)\Big]\Delta_pu
=\lambda f(x,u)+|u|^{p^\star-2}u\quad\hbox{in }\Omega,\cr
u=0\quad\hbox{on }\partial\Omega,
}$$](gifs/aa.gif)
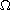 is a bounded smooth domain of
is a bounded smooth domain of
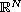 ,
,
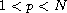 ,
,
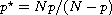 is the critical Sobolev
exponent,
is the critical Sobolev
exponent,
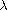 is a positive parameter, f and g are
continuous functions. The main results of this paper establish, via
the variational method. The concentration-compactness principle
allows to prove that the Palais-Smale condition is satisfied below a
certain level.
is a positive parameter, f and g are
continuous functions. The main results of this paper establish, via
the variational method. The concentration-compactness principle
allows to prove that the Palais-Smale condition is satisfied below a
certain level.


