In a connected finite graph
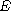 with set of vertices
with set of vertices
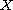 ,
choose a nonempty subset, not equal to
the whole set,
,
choose a nonempty subset, not equal to
the whole set,
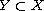 ,
and call it the boundary
,
and call it the boundary
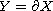 .
Given a real-valued function
.
Given a real-valued function
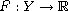 , our objective
is to find a function
, our objective
is to find a function
 , such that
, such that
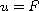 on
on
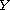 , and
for all
, and
for all
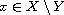 ,
,
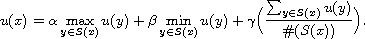
Here
 are non-negative constants such that
are non-negative constants such that
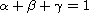 , the set
, the set
 is the collection of vertices connected to
is the collection of vertices connected to
 by an edge, and
by an edge, and
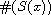 denotes its cardinality.
We prove the existence and uniqueness of a solution of the above
Dirichlet problem and study the qualitative properties of the solution.
denotes its cardinality.
We prove the existence and uniqueness of a solution of the above
Dirichlet problem and study the qualitative properties of the solution.
