Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 73, pp. 1-9.
Entire solutions for a nonlinear differential equation
Jianming Qi, Jie Ding, Taiying Zhu
Abstract:
In this article, we study the existence of solutions to
the differential equation
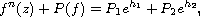
where
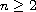 is an positive integer, f is a transcendental
entire function,
is an positive integer, f is a transcendental
entire function,
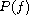 is a differential polynomial in f of
degree less than or equal n-1,
is a differential polynomial in f of
degree less than or equal n-1,
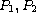 are small functions
of
are small functions
of
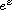 ,
,
 ,
,
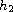 are polynomials, and
are polynomials, and
 is in the open
complex plane
is in the open
complex plane
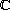 .
Our results extend those obtained by Li [6,7,8].
.
Our results extend those obtained by Li [6,7,8].
Submitted July 10, 2010. Published June 15, 2011.
Math Subject Classifications: 30D35, 30D45.
Key Words: Transcendental entire functions; Nevanlinna theory;
differential equations.
Show me the PDF file (226 KB),
TEX file for this article.
 |
Jianming Qi
Department of Mathematics and Physics
Shanghai Dianji University
Shanghai 200240, China
email: qijianming1981@gmail.com
|
|---|
 |
Jie Ding
Department of Mathematics, Shandong University
Jinan 250100, China
email: dingjie169@163.com
|
|---|
 |
Taiying Zhu
Department of Mathematics and Physics
Shanghai Dianji University
Shanghai 200240, China
email: ztyyyy@163.com
|
|---|
Return to the EJDE web page
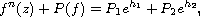
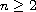 is an positive integer, f is a transcendental
entire function,
is an positive integer, f is a transcendental
entire function,
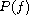 is a differential polynomial in f of
degree less than or equal n-1,
is a differential polynomial in f of
degree less than or equal n-1,
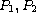 are small functions
of
are small functions
of
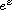 ,
,
 ,
,
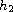 are polynomials, and
are polynomials, and
 is in the open
complex plane
is in the open
complex plane
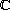 .
Our results extend those obtained by Li [6,7,8].
.
Our results extend those obtained by Li [6,7,8].


