Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 104, pp. 1-10.
Existence of scale invariant solutions to horizontal flow with a
Fujita type diffusion coefficient
Gastao A. Braga, Paulo C. Carriao, Antonio A. G. Ruas
Abstract:
In this article, we study a boundary-initial value problem on the half-line
for the diffusion equation with a Fujita type diffusion coefficient
that carries a parameter
 .
The equation models
the flow of water in soil within an approximation where gravitational
effects are not taken into account and, when
.
The equation models
the flow of water in soil within an approximation where gravitational
effects are not taken into account and, when
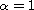 ,
an explicit
self-similar solution
,
an explicit
self-similar solution
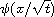 can be found.
We prove that if
can be found.
We prove that if
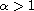 then the above problem, with
uniform boundary conditions, posses self-similar solutions.
This is the first step towards a multiscale (renormalization group)
asymptotic analysis of solutions to more general equations than the ones
studied here.
then the above problem, with
uniform boundary conditions, posses self-similar solutions.
This is the first step towards a multiscale (renormalization group)
asymptotic analysis of solutions to more general equations than the ones
studied here.
Submitted October 11, 2011. Published June 21, 2012.
Math Subject Classifications: 34E10, 34E13, 35C06, 35Q86.
Key Words: Water infiltration; nonlinear diffusion; self-similar solutions;
Fujita diffusion coefficient.
Show me the PDF file (236 KB),
TEX file for this article.
 |
Gastão A. Braga
Departamento de Matemática - UFMG,
Caixa Postal 1621
30161-970 Belo Horizonte, MG, Brazil
email: gbraga@mat.ufmg.br
|
|---|
 |
Paulo C. Carrião
Departamento de Matemática - UFMG,
Caixa Postal 1621
30161-970 Belo Horizonte, MG, Brazil
email: carrion@mat.ufmg.br
|
|---|
 |
Antonio A. G. Ruas
Departamento de Matemática - UFMG,
Caixa Postal 1621
30161-970 Belo Horizonte, MG, Brazil
email: gaspar@mat.ufmg.br
|
|---|
Return to the EJDE web page
 .
The equation models
the flow of water in soil within an approximation where gravitational
effects are not taken into account and, when
.
The equation models
the flow of water in soil within an approximation where gravitational
effects are not taken into account and, when
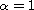 ,
an explicit
self-similar solution
,
an explicit
self-similar solution
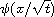 can be found.
We prove that if
can be found.
We prove that if
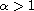 then the above problem, with
uniform boundary conditions, posses self-similar solutions.
This is the first step towards a multiscale (renormalization group)
asymptotic analysis of solutions to more general equations than the ones
studied here.
then the above problem, with
uniform boundary conditions, posses self-similar solutions.
This is the first step towards a multiscale (renormalization group)
asymptotic analysis of solutions to more general equations than the ones
studied here.


