We study the global structure of the set of radial solutions of a nonlinear Dirichlet eigenvalue problem involving the p-Laplacian with p>2, in the unit ball of
,
.
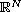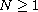We show that all non-trivial radial
solutions lie on smooth curves of respectively positive and negative solutions,
bifurcating from the first eigenvalue of a weighted p-linear problem.
Our approach involves a local bifurcation result of Crandall-Rabinowitz type,
and global continuation arguments relying on monotonicity properties of the
equation.
An important part of the analysis is dedicated to the delicate issue of
differentiability of the inverse p-Laplacian, and holds for all p>1.
