Electron. J. Diff. Equ., Vol. 2012 (2012), No. 125, pp. 1-6.

On Pacard's regularity for the equation $-\Delta u = u^p$

David R. Adams

Abstract:
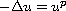It is shown that the singular set for a positive solution of the PDE $-\Delta u = u^p$ has Hausdorff dimension less than or equal to $n - 2p'$, as conjectured by Pacard [12] in 1993.

Submitted June 4, 2012. Published August 2, 2012.
Math Subject Classifications: 35D10, 35J60.
Key Words: Weak solutions; singular set; regularity.

Show me the PDF file (202 KB), TEX file, and other files for this article.

David R. Adams
Department of Mathematics
University of kentucky, POT 714
Lexington, KY 40506, USA
email: dave@ms.uky.edu

Return to the EJDE web page