We consider the eigenvalue problem for the equation
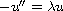 on
on
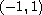 ,
together with general Sturm-Liouville-type, multi-point boundary
conditions at
,
together with general Sturm-Liouville-type, multi-point boundary
conditions at
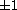 .
We show that the basic spectral properties of this problem are similar
to those of the standard Sturm-Liouville problem with separated boundary
conditions.
In particular, for each integer
.
We show that the basic spectral properties of this problem are similar
to those of the standard Sturm-Liouville problem with separated boundary
conditions.
In particular, for each integer
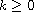 there exists a unique, simple
eigenvalue
there exists a unique, simple
eigenvalue
 whose eigenfunctions have 'oscillation count'
equal to k.
Similar multi-point problems have been considered before
for Dirichlet-type or Neumann-type multi-point boundary
conditions, or a mixture of these.
Different oscillation counting methods have been used in each of these
cases. A new oscillation counting method is used here which unifies and
extends all the results for these special case to the general
Sturm-Liouville-type boundary conditions.
whose eigenfunctions have 'oscillation count'
equal to k.
Similar multi-point problems have been considered before
for Dirichlet-type or Neumann-type multi-point boundary
conditions, or a mixture of these.
Different oscillation counting methods have been used in each of these
cases. A new oscillation counting method is used here which unifies and
extends all the results for these special case to the general
Sturm-Liouville-type boundary conditions.
