In this article, we study the second-order three-point boundary-value problem

where
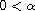 ,
,
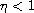 ,
,
![$a\in C([0,1],(-\infty, 0))$](gifs/ad.gif) and
and
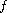 is
allowed to change sign. We show that there exist two positive
solutions by using Leggett-Williams fixed-point theorem.
is
allowed to change sign. We show that there exist two positive
solutions by using Leggett-Williams fixed-point theorem.
Jian Liu, Zengqin Zhao
Abstract:
In this article, we study the second-order three-point boundary-value
problem

where
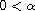 ,
,
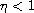 ,
,
![$a\in C([0,1],(-\infty, 0))$](gifs/ad.gif) and
and
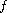 is
allowed to change sign. We show that there exist two positive
solutions by using Leggett-Williams fixed-point theorem.
is
allowed to change sign. We show that there exist two positive
solutions by using Leggett-Williams fixed-point theorem.
Submitted March 14, 2012. Published September 7, 2012.
Math Subject Classifications: 34B15, 34B25.
Key Words: Multiple positive solutions; sign changing; fixed-point theorem.
Show me the PDF file (204 KB), TEX file for this article.
 |
Jian Liu School of Mathematics and Quantitative Economics Shandong University of Finance and Economics Jinan, Shandong, 250014, China email: liujianmath@163.com |
|---|---|
 |
Zengqin Zhao School of Mathematical Sciences Qufu Normal University, Qufu Shandong, 273165, China email: zqzhao@mail.qfnu.edu.cn |
Return to the EJDE web page