Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 207, pp. 1-22.
Regularity of random attractors for stochastic semilinear
degenerate parabolic equations
Cung The Anh, Tang Quoc Bao, Nguyen Van Thanh
Abstract:
We consider the stochastic semilinear degenerate parabolic equation
![$$
du+[- \operatorname{div}(\sigma(x)\nabla u) + f(u) + \lambda u]dt
= gdt+ \sum_{j=1}^{m}h_j{d\omega_j}
$$](gifs/aa.gif)
in a bounded domain
 , with the nonlinearity
satisfies an arbitrary polynomial growth condition.
The random dynamical system generated by the equation is shown
to have a random attractor
, with the nonlinearity
satisfies an arbitrary polynomial growth condition.
The random dynamical system generated by the equation is shown
to have a random attractor
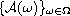 in
in
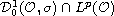 .
The results obtained improve some recent ones for stochastic
semilinear degenerate parabolic equations.
.
The results obtained improve some recent ones for stochastic
semilinear degenerate parabolic equations.
Submitted September 27, 2012. Published November 25, 2012.
Math Subject Classifications: 35B41, 37H10, 35K65.
Key Words: Random dynamical systems; random attractors; regularity;
stochastic degenerate parabolic equations;
asymptotic a priori estimate method.
Show me the PDF file (341 KB),
TEX file for this article.
 |
Cung The Anh
Department of Mathematics
Hanoi National Univiersity of Education
136 Xuan Thuy, Cau Giay, Hanoi, Vietnam
email: anhctmath@hnue.edu.vn
|
|---|
 |
Tang Quoc Bao
School of Applied Mathematics and Informatics
Hanoi University of Science and Technology
1 Dai Co Viet, Hai Ba Trung, Hanoi, Vietnam
email: baotangquoc@gmail.com
|
|---|
 |
Nguyen Van Thanh
Foreign Languages Specialized School
University Of Languages and International Studies
Hanoi National University
2 Pham Van Dong, Cau Giay, Hanoi, Vietnam
email: thanhnvmath@gmail.com
|
|---|
Return to the EJDE web page
![$$
du+[- \operatorname{div}(\sigma(x)\nabla u) + f(u) + \lambda u]dt
= gdt+ \sum_{j=1}^{m}h_j{d\omega_j}
$$](gifs/aa.gif)
 , with the nonlinearity
satisfies an arbitrary polynomial growth condition.
The random dynamical system generated by the equation is shown
to have a random attractor
, with the nonlinearity
satisfies an arbitrary polynomial growth condition.
The random dynamical system generated by the equation is shown
to have a random attractor
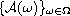 in
in
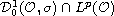 .
The results obtained improve some recent ones for stochastic
semilinear degenerate parabolic equations.
.
The results obtained improve some recent ones for stochastic
semilinear degenerate parabolic equations.


