Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 208, pp. 1-11.
Existence of positive solutions for nonlinear fractional systems
in bounded domains
Imed Bachar
Abstract:
We prove the existence of positive continuous solutions to the nonlinear
fractional system
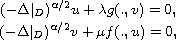
in a bounded
 -domain
-domain
 in
in
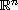
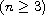 ,
subject to Dirichlet conditions, where
,
subject to Dirichlet conditions, where
 ,
,
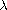 and
and
 are nonnegative parameters. The functions f and g are
nonnegative continuous monotone with respect to the second variable
and satisfying certain hypotheses related to the Kato class.
are nonnegative parameters. The functions f and g are
nonnegative continuous monotone with respect to the second variable
and satisfying certain hypotheses related to the Kato class.
Submitted September 8, 2012. Published November 25, 2012.
Math Subject Classifications: 35J60, 34B27, 35B44.
Key Words: Fractional nonlinear systems; Green function;
positive solutions; blow-up solutions
Show me the PDF file (245 KB),
TEX file for this article.
 |
Imed Bachar
King Saud University College of Science Mathematics
Department P.O. Box 2455
Riyadh 11451 Kingdom of Saudi Arabia
email: abachar@ksu.edu.sa
|
|---|
Return to the EJDE web page
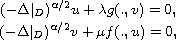
 -domain
-domain
 in
in
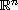
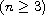 ,
subject to Dirichlet conditions, where
,
subject to Dirichlet conditions, where
 ,
,
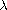 and
and
 are nonnegative parameters. The functions f and g are
nonnegative continuous monotone with respect to the second variable
and satisfying certain hypotheses related to the Kato class.
are nonnegative parameters. The functions f and g are
nonnegative continuous monotone with respect to the second variable
and satisfying certain hypotheses related to the Kato class.
