In this article, we study the existence of nonnegative solutions for the elliptic partial differential equation
![$$\displaylines{
-[M(\|u\|^{p}_{1,p})]^{1,p}\Delta_{p}u = f(x,u)
\quad\hbox{in } \Omega , \cr
u = 0 \quad\hbox{on } \partial\Omega ,
}$$](gifs/aa.gif)
where
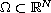 is a bounded smooth domain,
is a bounded smooth domain,
 is
a discontinuous nonlinear function.
is
a discontinuous nonlinear function.
Francisco Julio S. A. Correa, Rubia G. Nascimento
Abstract:
In this article, we study the existence of nonnegative
solutions for the elliptic partial differential equation
![$$\displaylines{
-[M(\|u\|^{p}_{1,p})]^{1,p}\Delta_{p}u = f(x,u)
\quad\hbox{in } \Omega , \cr
u = 0 \quad\hbox{on } \partial\Omega ,
}$$](gifs/aa.gif)
where
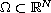 is a bounded smooth domain,
is a bounded smooth domain,
 is
a discontinuous nonlinear function.
is
a discontinuous nonlinear function.
Submitted October 12, 2011. Published February 7, 2012.
Math Subject Classifications: 35A15, 35J40, 34A36.
Key Words: Variational methods; elliptic problem;
discontinuous nonlinearity.
Show me the PDF file (252 KB), TEX file for this article.
 |
Francisco Julio S. A. Corrêa Universidade Federal de Campina Grande Unidade Acadêmica de Matemática e Estatística CEP:58109-970, Campina Grande-PB, Brazil email: fjsacorrea@gmail.com |
|---|---|
 |
Rubia G. Nascimento Faculdade de Matemática Universidade Federal do Pará CEP:66075-110, Belém -PA, Brazil email: rubia@ufpa.br |
Return to the EJDE web page