Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 220, pp. 1-13.
Anisotropic problems with variable exponents and
constant Dirichlet conditions
Maria-Magdalena Boureanu, Cristian Udrea, Diana-Nicoleta Udrea
Abstract:
We study a general class of anisotropic problems involving
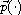 -Laplace
type operators.
We search for weak solutions that are constant on the boundary
by introducing a new subspace of the anisotropic Sobolev space with
variable exponent and by proving that it is a reflexive Banach space.
Our argumentation for the existence of weak solutions is mainly based
on a variant of the mountain pass theorem of Ambrosetti and Rabinowitz.
-Laplace
type operators.
We search for weak solutions that are constant on the boundary
by introducing a new subspace of the anisotropic Sobolev space with
variable exponent and by proving that it is a reflexive Banach space.
Our argumentation for the existence of weak solutions is mainly based
on a variant of the mountain pass theorem of Ambrosetti and Rabinowitz.
Submitted April 8, 2013. Published October 4, 2013.
Math Subject Classifications: 35J25, 46E35, 35D30, 35J20.
Key Words: Anisotropic variable exponent Sobolev spaces;
Dirichlet problem; existence of weak solutions; mountain pass theorem.
A corrigendum was posted on December 23, 2013. It adds a condition to
the original problem, and adds six references. See the last page of this article.
Show me the PDF file (259 KB),
TEX file for this article.
 |
Maria-Magdalena Boureanu
Department of Applied Mathematics
University of Craiova
200585 Craiova, Romania
email: mmboureanu@yahoo.com
|
|---|
 |
Cristian Udrea
Department of Applied Mathematics
University of Craiova
200585 Craiova, Romania
email: udrea.cristian2013@yahoo.com
|
|---|
 |
Diana-Nicoleta Udrea
Department of Mathematics
University of Craiova
200585 Craiova, Romania
email: diannannicole@yahoo.com
|
|---|
Return to the EJDE web page
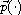 -Laplace
type operators.
We search for weak solutions that are constant on the boundary
by introducing a new subspace of the anisotropic Sobolev space with
variable exponent and by proving that it is a reflexive Banach space.
Our argumentation for the existence of weak solutions is mainly based
on a variant of the mountain pass theorem of Ambrosetti and Rabinowitz.
-Laplace
type operators.
We search for weak solutions that are constant on the boundary
by introducing a new subspace of the anisotropic Sobolev space with
variable exponent and by proving that it is a reflexive Banach space.
Our argumentation for the existence of weak solutions is mainly based
on a variant of the mountain pass theorem of Ambrosetti and Rabinowitz.


