Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 28, pp. 1-8.
The barrier strip technique for a boundary value problem with p-Laplacian
Petio S. Kelevedjiev, Stepan A. Tersian
Abstract:
We study the solvability of the boundary value problem

where
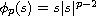 ,
using the barrier strip type arguments.
We establish the existence of
,
using the barrier strip type arguments.
We establish the existence of
![$C^2[0,1]$](gifs/ac.gif) -solutions,
restricting our
considerations to
-solutions,
restricting our
considerations to
![$p\in(1,2]$](gifs/ad.gif) .
The existence of positive monotone
solutions is also considered.
.
The existence of positive monotone
solutions is also considered.
Submitted June 27, 2012. Published January 28, 2013.
Math Subject Classifications: 34B15, 34B18.
Key Words: Boundary value problem; second order differential equation;
p-Laplacian, sign condition
Show me the PDF file (203 KB),
TEX file for this article.
 |
Petio S. Kelevedjiev
Department of Mathematics
Technical University of Sliven
Sliven, Bulgaria
email: keleved@mailcity.com
|
|---|
 |
Stepan A. Tersian
Department of Mathematical Analysis
University of Ruse,
Ruse, Bulgaria
email: sterzian@uni-ru.acad.bg
|
|---|
Return to the EJDE web page

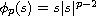 ,
using the barrier strip type arguments.
We establish the existence of
,
using the barrier strip type arguments.
We establish the existence of
![$C^2[0,1]$](gifs/ac.gif) -solutions,
restricting our
considerations to
-solutions,
restricting our
considerations to
![$p\in(1,2]$](gifs/ad.gif) .
The existence of positive monotone
solutions is also considered.
.
The existence of positive monotone
solutions is also considered.

