Let
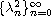 be the spectra of a Sturm-Liouville problem on
be the spectra of a Sturm-Liouville problem on
![$[0,\pi ]$](gifs/ab.gif) .
We investigate the question:
Do the systems
.
We investigate the question:
Do the systems
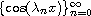 or
or
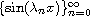 form Riesz bases in
form Riesz bases in
![${L^2}[0,\pi ]$](gifs/ae.gif) ?
The answer is almost always positive.
?
The answer is almost always positive.
Tigran Harutyunyan, Avetik Pahlevanyan, Anna Srapionyan
Abstract:
Let
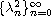 be the spectra of a Sturm-Liouville problem on
be the spectra of a Sturm-Liouville problem on
![$[0,\pi ]$](gifs/ab.gif) .
We investigate the question:
Do the systems
.
We investigate the question:
Do the systems
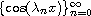 or
or
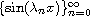 form Riesz bases in
form Riesz bases in
![${L^2}[0,\pi ]$](gifs/ae.gif) ?
The answer is almost always positive.
?
The answer is almost always positive.
Submitted November 19, 2012. Published March 17, 2013.
Math Subject Classifications: 34B24, 42C15, 34L10.
Key Words: Sturm-Liouville problem; eigenvalues; Riesz bases.
Show me the PDF file (199 KB), TEX file for this article.
 |
Tigran Harutyunyan Faculty of Mathematics and Mechanics, Yerevan State University 1 Alex Manoogian, 0025, Yerevan, Armenia email: hartigr@yahoo.co.uk |
|---|---|
 |
Avetik Pahlevanyan Faculty of Mathematics and Mechanics, Yerevan State University 1 Alex Manoogian, 0025, Yerevan, Armenia email: avetikpahlevanyan@gmail.com |
 |
Anna Srapionyan Faculty of Mathematics and Mechanics, Yerevan State University 1 Alex Manoogian, 0025, Yerevan, Armenia email: srapionyan.anna@gmail.com |
Return to the EJDE web page