Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 142, pp. 1-17.
Continuous evolution of equations and inclusions involving set-valued
contraction mappings with applications to generalized fractal transforms
Herb Kunze, Davide La Torre, Franklin Mendivil, Edward R. Vrscay
Abstract:
Let T be a set-valued contraction mapping on a general Banach space
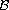 .
In the first part of this paper we introduce the evolution
inclusion
.
In the first part of this paper we introduce the evolution
inclusion
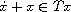 and study the convergence of solutions
to this inclusion toward fixed points of T.
Two cases are examined:
and study the convergence of solutions
to this inclusion toward fixed points of T.
Two cases are examined:
(i) T has a fixed point
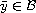 in the usual sense, i.e.,
in the usual sense, i.e.,
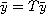 and
and
(ii) T has a fixed point in the sense of inclusions, i.e.,
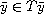 .
In the second part we extend this analysis to the case of set-valued
evolution equations taking the form
.
In the second part we extend this analysis to the case of set-valued
evolution equations taking the form
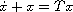 .
We also provide some applications to generalized fractal transforms.
.
We also provide some applications to generalized fractal transforms.
Submitted July 16, 2013. Published June 18, 2014.
Math Subject Classifications: 34A60, 28A80.
Key Words: Set-valued evolution inclusions, set-valued evolution equations,
contractive set-valued functions, fixed points.
Show me the PDF file (337 KB),
TEX file for this article.
 |
Herb Kunze
Department of Mathematics and Statistics
University of Guelph, Guelph, Ontario, Canada
email: hkunze@uoguelph.ca
|
|---|
 |
Davide La Torre
Department of Economics, Management, and Quantitative Methods
University of Milan, Milan, Italy.
email: davide.latorre@unimi.it, davide.latorre@kustar.ac.ae
|
|---|
 |
Franklin Mendivil
Department of Mathematics and Statistics, Acadia University
Wolfville, Nova Scotia, Canada
email: franklin.mendivil@acadiau.ca
|
|---|
 |
Edward R. Vrscay
Department of Applied Mathematics, Faculty of Mathematics
University of Waterloo, Waterloo, Ontario, Canada
email: ervrscay@uwaterloo.ca
|
|---|
Return to the EJDE web page
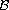 .
In the first part of this paper we introduce the evolution
inclusion
.
In the first part of this paper we introduce the evolution
inclusion
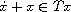 and study the convergence of solutions
to this inclusion toward fixed points of T.
Two cases are examined:
and study the convergence of solutions
to this inclusion toward fixed points of T.
Two cases are examined: 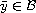 in the usual sense, i.e.,
in the usual sense, i.e.,
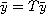 and
and 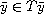 .
In the second part we extend this analysis to the case of set-valued
evolution equations taking the form
.
In the second part we extend this analysis to the case of set-valued
evolution equations taking the form
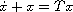 .
We also provide some applications to generalized fractal transforms.
.
We also provide some applications to generalized fractal transforms.



