In this article, we study the nonlinear elliptic problem of
 -
-
 -Laplacian type
-Laplacian type
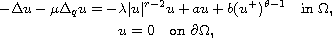
where
 is a bounded
domain. For a is between two eigenvalues, we show the existence of three
nontrivial solutions.
is a bounded
domain. For a is between two eigenvalues, we show the existence of three
nontrivial solutions.
Dandan Yang, Chuanzhi Bai
Abstract:
In this article, we study the nonlinear elliptic
problem of
 -
-
 -Laplacian type
-Laplacian type
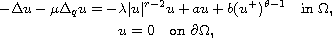
where
 is a bounded
domain. For a is between two eigenvalues, we show the existence of three
nontrivial solutions.
is a bounded
domain. For a is between two eigenvalues, we show the existence of three
nontrivial solutions.
Submitted July 9, 2014. Published August 11, 2014.
Math Subject Classifications: 35J60, 35B38.
Key Words: Quasilinear elliptic equations with q-Laplacian; critical exponent;
asymmetric nonlinearity; weak solution.
Show me the PDF file (263 KB), TEX file for this article.
 |
Dandan Yang School of Mathematical Science, Huaiyin Normal University Huaian, Jiangsu 223300, China email: ydd423@sohu.com |
|---|---|
 |
Chuanzhi Bai School of Mathematical Science, Huaiyin Normal University Huaian, Jiangsu 223300, China email: czbai@hytc.edu.cn |
Return to the EJDE web page