In this article, we study the blow up behavior of the heat equation
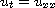 with
with
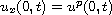 ,
,
 .
We also study the quenching behavior of the nonlinear parabolic equation
.
We also study the quenching behavior of the nonlinear parabolic equation
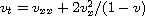 with
with
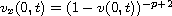 ,
,
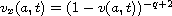 .
In the blow up problem, if
.
In the blow up problem, if
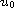 is a lower solution then we get the blow up occurs in a finite time at the
boundary
is a lower solution then we get the blow up occurs in a finite time at the
boundary
 and using positive steady state we give criteria for blow up
and non-blow up. In the quenching problem, we show that the only quenching
point is
and using positive steady state we give criteria for blow up
and non-blow up. In the quenching problem, we show that the only quenching
point is
 and
and
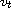 blows up at the quenching time, under certain
conditions and using positive steady state we give criteria for quenching
and non-quenching. These analysis is based on the equivalence between the
blow up and the quenching for these two equations.
blows up at the quenching time, under certain
conditions and using positive steady state we give criteria for quenching
and non-quenching. These analysis is based on the equivalence between the
blow up and the quenching for these two equations.
