Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 258, pp. 1-8.
Lp estimates for Dirichlet-to-Neumann operator and applications
Toufic El Arwadi, Toni Sayah
Abstract:
In this article, we consider the time dependent linear
elliptic problem with dynamic boundary condition. We recall the
corresponding Dirichlet-to-Neumann operator on
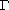 denoted by
denoted by
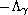 .
Then we show that when
.
Then we show that when
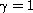 near the
boundary,
near the
boundary,
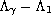 is bounded by
is bounded by
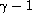 in
in
 norm. This result is a generalization of the bound
with the
norm. This result is a generalization of the bound
with the
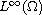 norm and is applicable for comparing the
Dirichlet to Neumann semigroup and the Lax semigroup. Finally, we
present numerical experiments for validation of our results.
norm and is applicable for comparing the
Dirichlet to Neumann semigroup and the Lax semigroup. Finally, we
present numerical experiments for validation of our results.
Submitted September 5, 2015. Published October 2, 2015.
Math Subject Classifications: 47D06, 47A99, 35J15, 35M13, 65M60.
Key Words: Dynamic boundary condition; Dirichlet-to-Neumann operator;
Lp estimation; finite element method.
Show me the PDF file (273 KB),
TEX file for this article.
 |
Toufic El Arwadi
Department of Mathematics and computer science
Faculty of Science, Beirut Arab university
P.O. Box: 11-5020, Beirut, Lebanon
email: t.elarwadi@bau.edu.lb
|
|---|
 |
Toni Sayah
Research unit "EGFEM", Faculty of sciences
Saint-Joseph University
B.P. 11-514 Riad El Solh
Beirut 1107 2050, Lebanon
email: toni.sayah@usj.edu.lb
|
|---|
Return to the EJDE web page
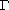 denoted by
denoted by
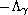 .
Then we show that when
.
Then we show that when
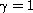 near the
boundary,
near the
boundary,
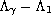 is bounded by
is bounded by
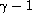 in
in
 norm. This result is a generalization of the bound
with the
norm. This result is a generalization of the bound
with the
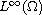 norm and is applicable for comparing the
Dirichlet to Neumann semigroup and the Lax semigroup. Finally, we
present numerical experiments for validation of our results.
norm and is applicable for comparing the
Dirichlet to Neumann semigroup and the Lax semigroup. Finally, we
present numerical experiments for validation of our results.

