Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 37, pp. 1-15.
Dynamics of the p-Laplacian equations with nonlinear
dynamic boundary conditions
Xiyou Cheng, Lei Wei
Abstract:
In this article, we study the long-time behavior of the p-Laplacian
equation with nonlinear dynamic boundary conditions for both
autonomous and non-autonomous cases. For the autonomous case, some
asymptotic regularity of solutions is proved. For the non-autonomous
case, we obtain the existence and structure of a compact uniform
attractor in
 (
(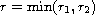 ).
).
Submitted May 6, 2014. Published February 10, 2015.
Math Subject Classifications: 37L05, 35B40, 35B41.
Key Words: p-Laplacian equation; boundary condition;
asymptotic regularity; attractor.
Show me the PDF file (296 KB),
TEX file for this article.
Xiyou Cheng
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: chengxy@lzu.edu.cn
|
Lei Wei
School of Mathematics and Statistics
Jiangsu Normal University
Xuzhou 221116, China
email: wlxznu@163.com
|
Return to the EJDE web page
 (
( ).
).