Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 151, pp. 1-12.
Multiple solutions for a fractional p-Laplacian equation with
sign-changing potential
Vincenzo Ambrosio
Abstract:
We use a variant of the fountain Theorem to prove the existence of infinitely
many weak solutions for the fractional p-Laplace equation

where
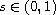 ,
,
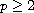 ,
,
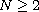 ,
,
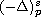 is the
fractional p-Laplace operator, the nonlinearity f is p-superlinear
at infinity and the potential V(x) is allowed to be sign-changing.
is the
fractional p-Laplace operator, the nonlinearity f is p-superlinear
at infinity and the potential V(x) is allowed to be sign-changing.
Submitted May 10, 2016. Published June 20, 2016.
Math Subject Classifications: 35A15, 35R11, 35J92.
Key Words: Fractional p-Laplacian; sign-changing potential; fountain theorem.
Show me the PDF file (258 KB),
TEX file for this article.
 |
Vincenzo Ambrosio
Dipartimento di Matematica e Applicazioni "R. Caccioppoli"
Università degli Studi di Napoli Federico II
via Cinthia, 80126 Napoli, Italy
email: vincenzo.ambrosio2@unina.it
|
|---|
Return to the EJDE web page

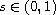 ,
,
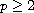 ,
,
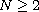 ,
,
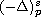 is the
fractional p-Laplace operator, the nonlinearity f is p-superlinear
at infinity and the potential V(x) is allowed to be sign-changing.
is the
fractional p-Laplace operator, the nonlinearity f is p-superlinear
at infinity and the potential V(x) is allowed to be sign-changing.
